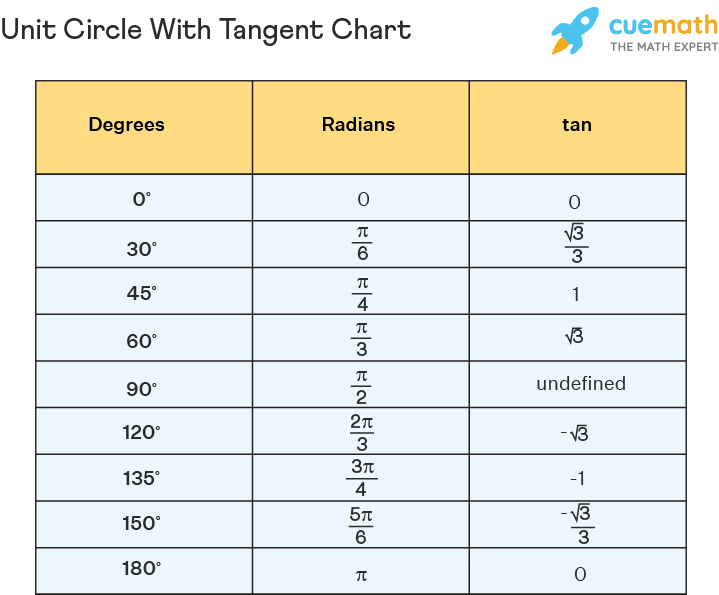
Let's dive into the magical world of trigonometry, where the unit circle with tangent rules the game. If you're a math lover or someone trying to survive your math class, this article's got your back. We're breaking down everything you need to know about the unit circle and its tangent relationship in a way that's easy to digest, even for those who think math is just a bunch of numbers and formulas. So, buckle up and get ready for a fun ride through the land of angles, radians, and tangents!
Now, you might be wondering, "Why should I care about the unit circle with tangent?" Well, my friend, this concept is like the secret sauce in trigonometry. It helps you solve all sorts of problems, from calculating distances on a map to understanding how waves work in physics. Plus, it's just plain cool once you wrap your head around it. Stick with me, and we'll make it as painless as possible.
Before we dive deep into the nitty-gritty, let's set the stage. The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane. It's like the home base for trigonometric functions, and when you throw tangent into the mix, things get really interesting. Trust me, by the end of this article, you'll be able to explain this stuff to your friends like a pro. So, let's get started!
Read also:Puppy Girlfriend The Cutest Trend Thatrsquos Taking The World By Storm
What is the Unit Circle Anyway?
Alright, first things first. The unit circle is not some mystical object; it's actually pretty straightforward. Imagine a circle drawn on a graph, with its center right at the point (0,0). The radius of this circle is exactly one unit long, hence the name "unit circle." It's like the perfect circle, the golden standard of circles in the math world.
So, why is the unit circle so important in trigonometry? Well, it's because it helps us define the values of sine, cosine, and tangent for any angle. These functions are the building blocks of trigonometry, and the unit circle makes it super easy to visualize and understand them. Think of the unit circle as your trusty map for navigating the world of angles.
How Does the Unit Circle Work?
Here's the basic idea: every point on the unit circle corresponds to a specific angle. You measure the angle starting from the positive x-axis and moving counterclockwise. The coordinates of each point on the circle give you the cosine and sine values for that angle. Cool, right? It's like a treasure map where the treasure is mathematical understanding.
Introducing Tangent into the Mix
Now that we've got the unit circle down, let's talk about tangent. Tangent is one of the trigonometric functions, and it's defined as the ratio of sine to cosine. In the context of the unit circle, tangent tells us the slope of the line that passes through the origin and the point on the circle corresponding to a given angle.
One important thing to note is that tangent is undefined at certain angles, like 90 degrees and 270 degrees. Why? Because at those angles, the cosine value is zero, and division by zero is a big no-no in math. But don't worry, we'll cover all the details as we go along.
Why Tangent Matters in the Unit Circle
Tangent adds another layer of depth to the unit circle. While sine and cosine give you the x and y coordinates of a point on the circle, tangent gives you the slope of the line connecting that point to the origin. This is super useful in all sorts of applications, from physics to engineering to computer graphics. Essentially, tangent helps you understand how things change as you move around the circle.
Read also:Travis County Expo Center Your Ultimate Guide To The Heart Of Texas Events
Understanding the Relationship Between Unit Circle and Tangent
So, how exactly do the unit circle and tangent work together? It's all about the angles. For any angle on the unit circle, you can calculate the tangent value by dividing the sine value by the cosine value. This gives you a numerical representation of the slope at that point.
Let's break it down with an example. Say you've got an angle of 45 degrees. On the unit circle, the coordinates for this angle are (√2/2, √2/2). To find the tangent value, you divide the y-coordinate by the x-coordinate, which gives you 1. That means the slope of the line at this angle is 1, or in other words, the line rises one unit for every unit it runs.
Key Points to Remember
- Tangent is calculated as sine divided by cosine.
- Tangent is undefined when cosine is zero.
- The tangent value represents the slope of the line connecting the origin to a point on the unit circle.
Practical Applications of Unit Circle with Tangent
Now that we've covered the theory, let's talk about how the unit circle with tangent applies to real-world situations. Whether you're designing a roller coaster, analyzing sound waves, or programming a video game, understanding this concept can be incredibly useful.
For example, in physics, tangent helps you calculate the velocity of an object moving in a circular path. In engineering, it's used to design structures that can withstand forces from different directions. And in computer graphics, tangent is essential for creating realistic animations and visual effects. The possibilities are endless!
Examples of Unit Circle with Tangent in Action
Let's look at a couple of specific examples. Imagine you're building a bridge that needs to withstand wind forces from various angles. By using the unit circle with tangent, you can calculate the exact forces acting on the bridge at each angle and design it accordingly.
Or consider a sound engineer working on a concert. They use the unit circle with tangent to analyze how sound waves behave at different frequencies and angles, ensuring the best possible sound quality for the audience. These are just a few examples of how this mathematical concept has real-world impact.
Common Misconceptions About Unit Circle with Tangent
There are a few common misconceptions about the unit circle and tangent that can trip people up. One big one is thinking that tangent is only defined for angles between 0 and 90 degrees. In reality, tangent is defined for all angles, except where cosine is zero.
Another misconception is that the unit circle is only useful for math students. While it's true that it's a key concept in trigonometry, its applications extend far beyond the classroom. From navigation to architecture, the unit circle with tangent plays a vital role in many fields.
Clearing Up the Confusion
Here's a quick rundown of some key points to clear up any confusion:
- Tangent is defined for all angles except where cosine is zero.
- The unit circle is used in a wide range of fields, not just math.
- Tangent represents the slope of the line connecting the origin to a point on the circle.
Advanced Topics in Unit Circle with Tangent
If you're ready to take your understanding of the unit circle with tangent to the next level, there are plenty of advanced topics to explore. For example, you can delve into the derivatives of trigonometric functions, which are essential in calculus. Or you can explore complex numbers and how they relate to the unit circle.
Another fascinating area is Fourier analysis, where the unit circle with tangent is used to break down complex signals into simpler components. This has applications in everything from music production to telecommunications.
Where to Go from Here
If you're interested in diving deeper, there are plenty of resources available. Check out textbooks, online courses, and tutorials to expand your knowledge. And don't be afraid to experiment on your own – sometimes the best way to learn is by doing.
Conclusion: Wrapping It All Up
So, there you have it – the ultimate guide to the unit circle with tangent. We've covered everything from the basics to some advanced topics, and hopefully, you now have a solid understanding of this important concept. Remember, the unit circle with tangent isn't just a bunch of numbers and formulas; it's a powerful tool that has real-world applications in a variety of fields.
Now it's your turn to take action. Whether you're a student trying to ace your math class or a professional looking to apply this knowledge in your work, the unit circle with tangent is a valuable asset. Share this article with your friends, leave a comment with your thoughts, and don't forget to explore more articles on our site. Thanks for reading, and happy math-ing!
Table of Contents
- What is the Unit Circle Anyway?
- Introducing Tangent into the Mix
- Understanding the Relationship Between Unit Circle and Tangent
- Practical Applications of Unit Circle with Tangent
- Common Misconceptions About Unit Circle with Tangent
- Advanced Topics in Unit Circle with Tangent
- Conclusion: Wrapping It All Up